El tráfico es uno de los mayores problemas de la ciudad donde vive Rafael. Él cada día va de casa al trabajo durante la hora punta, a veces a velocidad muy lenta, lo que realmente le irrita. Es por eso que Rafael decide planificar con cuidado el mejor camino a seguir.

Todos los años dedicados a conducir por la ciudad le han permitido tener un mapa detallado con información del tráfico. Por sencillez, Rafael numera las diversas posiciones de la ciudad con números entre ~0~ y ~N-1~, siendo su casa la posición ~0~ y el trabajo la posición ~N-1~. El mapa contiene carreteras entre pares de posiciones, indicando para cada carretera la velocidad media en coche. Todas las carreteras son bidireccionales. El valor de un camino se define como la menor de las velocidades medias de sus carreteras. La figura siguiente ilustra un camino entre 0 (casa) y 8 (trabajo). Este camino pasa por las posiciones 0, 2, 4, 6 y 8, en este orden, y tiene un valor de 22 Km/h, el mínimo de las velocidades medias de sus carreteras, que son 40, 22, 28 y 50.

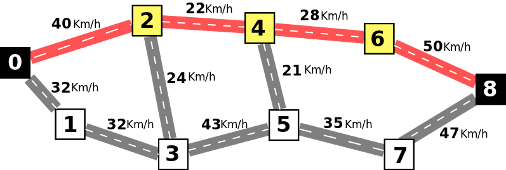
El siguiente camino, aunque sea más largo, es mejor, con un valor de 32 Km/h:

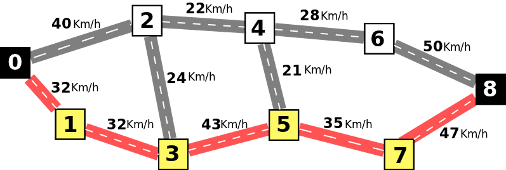
Rafael sabe que el alcalde tiene dinero para renovar carreteras. Una carretera renovada pasa a ser una avenida con dos carriles en cada sentido, lo que duplica su velocidad media. Por ejemplo, si se renueva la carretera entre 2 y 3, su velocidad media pasa a ser 48 Km/h, y es posible el camino siguiente con valor 35 Km/h (mejor que los anteriores):

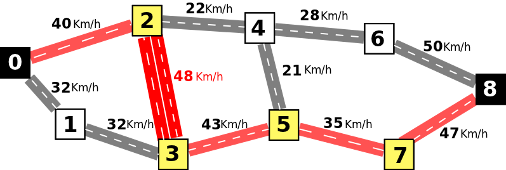
De hecho, el alcalde tiene dinero para renovar como mucho ~K~ carreteras. Como Rafael piensa que su propio camino es muy importante, decide enviar una carta al alcalde explicando qué carreteras deberían renovarse para conseguir el mejor camino para sí mismo. Por ejemplo, si ~K~ es 1, la figura anterior muestra el mejor escenario. Si ~K~ es 2, lo mejor es renovar las carreteras entre 2 y 4, y entre 4 y 6, consiguiendo un camino de valor 40Km/h:

¿Y en general? ¿Qué carreteras deben renovarse para conseguir el mejor camino para Rafael?

El Problema

Dado un mapa con ~N~ posiciones, un conjunto de ~E~ carreteras, con velocidades medias entre ~A~ y ~B~ definidas por ~V_{A,B}~, y el número ~K~ de carreteras que se pueden renovar, hay que calcular el valor del mejor camino posible desde la posición ~0~ (casa) hasta la posición ~N-1~ (trabajo), después de hacer como mucho ~K~ renovaciones.

Entrada

La primera línea contiene el número ~N~ de posiciones en el mapa. La segunda línea contiene el número ~E~ de carreteras. Luego vienen ~E~ líneas, cada una con tres enteros ~A B V_{A,B}~, separados con exactamente un espacio, indicando que hay una carretera entre ~A~ y ~B~ con velocidad media ~V_{A,B}~. Las carreteras pueden venir en cualquier orden, y nunca hay dos o más carreteras entre el mismo par de posiciones. No hay carreteras cuyo origen y final sea la misma posición y existe al menos un camino entre ~0~ y ~N-1~. Finalmente, la última línea contiene el número ~K~ the carreteras que pueden renovarse.

Salida

Una sola línea con un entero con el valor del mejor camino después de hacer como mucho ~K~ renovaciones. El valor de un camino es la mínima velocidad media de sus carreteras. El mejor camino es aquel con el máximo valor posible. Se puede escoger qué renovaciones hacer, pero cada carretera sólo se puede renovar una vez. Si ~K~ es cero, el resultado se corresponde con el mejor camino posible sin ninguna renovación.

Restricciones

Se garantizan los límites siguientes para todos los casos que se usarán para evaluar el programa:

• \(2 \leq N \leq 5 000\)    Número de posiciones en el mapa
• \(1 \leq E \leq 50 000\) Número de carreteras
• ~1 \leq V_{A,B} \leq 200~ Velocidad media de cada carretera
• ~0 \leq K \leq 20~ Cantidad de posibles renovaciones de carreteras

Nota sobre la Evaluación: Para un conjunto de casos que valen el 40% de los puntos, siempre se cumple ~N \leq 10~, ~E \leq 40~ y ~K \leq 1~.

Ejemplo de Entrada 1

9
11
0 2 40
2 4 22
4 6 28
6 8 50
0 1 32
1 3 32
3 5 43
5 7 35
7 8 47
2 3 24
4 5 21
1

Ejemplo de Salida 1

35

Ejemplo de Entrada 2

9
11
0 2 40
2 4 22
4 6 28
6 8 50
0 1 32
1 3 32
3 5 43
5 7 35
7 8 47
2 3 24
4 5 21
2

Ejemplo de Salida 2

40