Torre, Alfil y Rey

Points: 25 (partial)

Time limit: 1.0s

Memory limit: 64M

Author:

antonio_bouza

Problem type

Allowed languages

C, C++, Java, Pascal, Python

El pequeño Lucas está aprendiendo a jugar al ajedrez. Ya ha aprendido a mover un rey, una torre y un alfil. Permítanos recordarle las reglas para mover piezas de ajedrez. Un tablero de ajedrez tiene 64 casillas cuadradas organizadas en una tabla de $8$ ~8~× $8$ ~8~. Un casilla está representada por un par de números enteros ( $r$ ~r~, $c$ ~c~) – el número de la fila y el número de la columna (en un juego clásico, las columnas tradicionalmente están indexadas por letras). Cada pieza de ajedrez ocupa exactamente una casilla. Hacer un movimiento es mover una pieza de ajedrez, las piezas se mueven según las siguientes reglas:

Una torre se mueve cualquier número de casillas horizontal o verticalmente.
Un alfil se mueve cualquier número de casillas en diagonal.
Un rey se mueve una casilla en cualquier dirección: horizontal, vertical o diagonalmente.

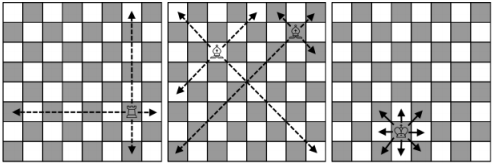
Lucas está pensando en el siguiente problema: ¿qué número mínimo de movimientos se necesita para que cada una de estas piezas pase de la casilla ( $r_1$ ~r_1~, $c_1$ ~c_1~) a la casilla ( $r_2$ ~r_2~, $c_2$ ~c_2~)? Para esto, asumimos que no hay más piezas además de éstas en el tablero. Ayúdalo a resolver este problema.

Entrada

La entrada contiene cuatro enteros $r_1$ ~r_1~, $c_1$ ~c_1~, $r_2$ ~r_2~, $c_2$ ~c_2~ $(1 \leq r_1, c_1, r_2, c_2 \leq 8)$ ~(1 \leq r_1, c_1, r_2, c_2 \leq 8)~ — las coordenadas de la casilla inicial y final. La casilla inicial no coincide con la final.

Puede suponer que las filas del tablero de ajedrez están numeradas de arriba a abajo del $1$ ~1~ al $8$ ~8~, y las columnas están numeradas de izquierda a derecha del $1$ ~1~ al $8$ ~8~.

Salida

Escriba tres enteros separados por espacios: el número mínimo de movimientos de la torre, el alfil y el rey (en este orden) que se necesita para pasar de la casilla ( $r_1$ ~r_1~, $c_1$ ~c_1~) a la casilla ( $r_2$ ~r_2~, $c_2$ ~c_2~). Si una pieza no puede hacer tal movimiento, imprima un $0$ ~0~ en lugar del número correspondiente.

Ejemplo de Entrada #1

4 3 1 6

Ejemplo de Salida #1

2 1 3

Ejemplo de Entrada #2

5 5 5 6

Ejemplo de Salida #2

1 0 1

Comments

-1

Luisito0101 commented on Dec. 17, 2024, 12:58 a.m.

1.e4 (solo los genios saben de que hablo)

-1

Daniel_Dosil commented on Dec. 18, 2024, 1:03 a.m.

1.e5