Una cadena poligonal consiste de ~n~ puntos ~p_1, p_2, \dots, p_n~ donde hay un segmento de línea entre dos puntos consecutivos.

Tu tarea es determinar si una cadena poligonal de ~n~ puntos puede ser rotada de tal manera que se convierta en una función. Debes responder ~q~ preguntas independientes.

Una función es una correspondencia entre dos conjuntos de tal manera que a cada elemento del primer conjunto le corresponde uno y sólo un elemento del segundo conjunto.

Subtareas

• Subtarea 1 (30 puntos): ~1 \le q \le 100~, ~2 \le n \le 1000~, ~-100 \le x,y \le 100~.
• Subtarea 2 (70 puntos): ~1 \le q \le 100~, ~2 \le n \le 10^6~, ~\sum n \le 10^6~, ~-10^9 \le x,y \le 10^9~.

Entrada

La primera línea de la entrada contiene un entero ~q~: la cantidad de preguntas. Después de esto las preguntas son dadas como sigue:

La primera línea de cada pregunta contiene un entero ~n~: el número de puntos. Luego, le siguen ~n~ líneas que contienen dos enteros cada una~(x_i, y_i)~: las coordenadas de los puntos de la cadena poligonal. Se asegura que no hay dos puntos consecutivos iguales, y no hay tres puntos consecutivos que se encuentren en la misma línea.

Salida

Por cada pregunta imprime la respuesta ("YES" o "NO") dependiendo de si la cadena poligonal puede ser representada como una función o no.

Ejemplos

Entrada 1

2
4
0 0
2 1
3 -1
2 -2
4
0 0
2 1
3 -1
2 0

Salida 1

YES
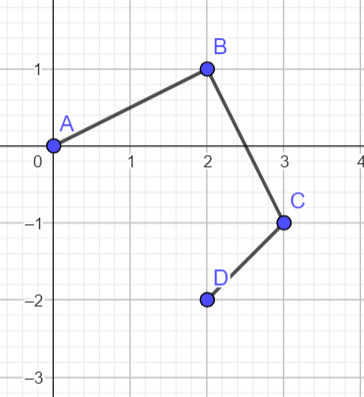
NO

La cadena poligonal de la primera pregunta es: