No todos saben que el perrito chill es un monstruo deborador de caramelos y le gustaba hacer más emocionante el proceso de comerlos de la siguiente forma:

1. El lanza un conjunto de caramelos sobre el piso, el cual consideraremos un plano cartesiano y cada caramelo como un par ~(x,y)~ casualmente nunca caen dos caramelos con el mismo valor de X ni de Y.

2. Luego escoge un caramelo cualquiera y se lo come.

3. Luego escoge otro caramelo que se encuentre a la izquierda y debajo del anterior seleccionado (formalmente suponiendo que se comió un caramelo ubicado en el par ordenado ~(x,y)~ el se puede comer cualquier otro caramelo ~(x_i,y_i)~ si y solo si ~x_i < x~ y ~y_i < y~).

4. Repite el paso anterior hasta que no tenga mas caramelos.

Tarea

Se te pide que digas de antemano cuantos caramelos se va a comer el perrito chill dada su distribución en el plano, puedes asumir que el perrito chill siempre se come los caramelos de forma óptima, en otras palabras el siempre se va a comer la mayor cantidad posible de caramelos.

Entrada

Los datos se te van a dar vía la entrada estándar.

La primera linea contiene un entero ~n~, la cantidad de caramelos.

A partir de ahi hay ~n~ lineas, cada una con dos enteros ~x~ e ~y~, la ubicación de cada uno de los caramelos.

Salida

Debes imprimir un único número entero. La cantidad de caramelos que se va a comer el perrito chill.

Restricciones

~1 \le n \le 2 \cdot 10^5~

~0 \le x_i, y_i \le 10^9~

Subtareas

1. (5 puntos) ~n \le 20~
2. (10 puntos) ~n \le 100~ Los valores en X de los caramelos van a ser una permutación de tamaño ~n~, y los valores en Y van a ser ~1,2,3...n~
3. (20 puntos) ~n \le 1000~
4. (65 puntos) Sin restricciones adicionales.

Ejemplo de entrada 1

4
1 2
2 3
3 1
4 4

Ejemplo de salida 1

3

Explicación del ejemplo 1

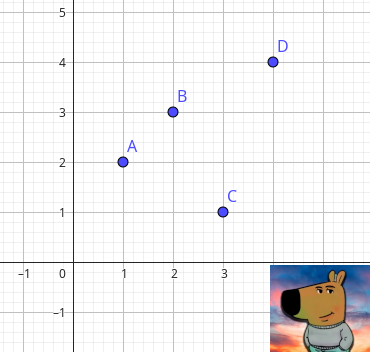
Lo óptimo sería comer primero el caramelo D, luego el caramelo B y luego el caramelo A, para un total de 3 caramelos.

Ejemplo de entrada 2

10
8 1
4 2
2 3
9 4
5 5
3 6
10 7
1 8
7 9
6 10

Ejemplo de salida 2

3

Explicación del ejemplo 2

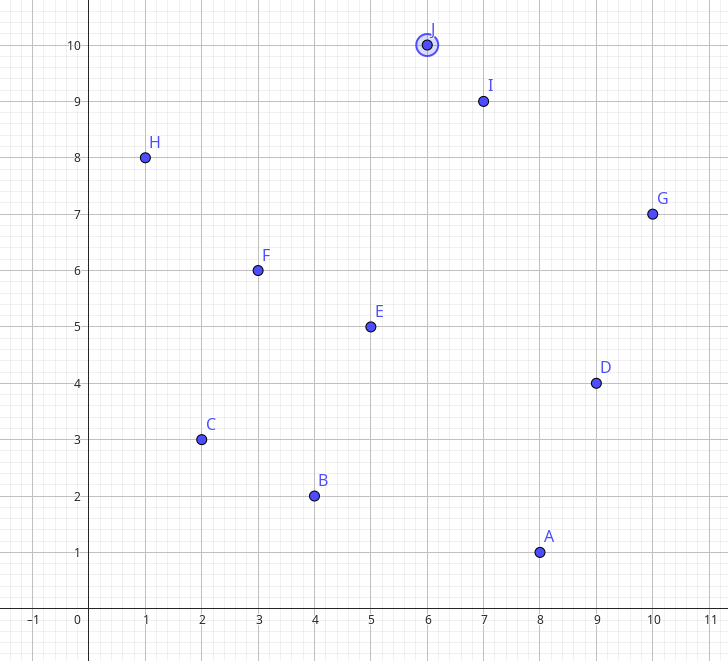
En este caso el perrito puede comer los caramelos de varias formas, pero lo maximo que comerá son tres. Podría por ejemplo comer primero el J luego el F y luego el C, para un total de 3 caramelos.

(Derecho de la imágen a Phillip Banks, su autor original)