Bessie tiene ~N~ ~( 3 \leq N \leq 40 )~ puntos favoritos distintos en una cuadrícula ~2D~, sin que hayan tres de ellos colineares. Para cada ~1 \leq i \leq N~, el punto ~i~-ésimo es denotado por dos enteros ~x_i~ y ~y_i~ ~( 0 \leq x_i,y_i \leq 10\,000 )~.

Bessie dibuja algunos segmentos entre los puntos como sigue:

1. Ella elije alguna permutación ~p_1,p_2,\ldots,p_N~ de los ~N~ puntos.
2. Dibuja segmentos entre ~p_1~ y ~p_2~, ~p_2~ y ~p_3~, y ~p_3~ y ~p_1~.
3. Luego para cada entero ~i~ de ~4~ a ~N~ en orden, dibuja un segmento de ~p_i~ a ~p_j~ para todo ~j < i~ tal que el segmento no intersecta ninguno de los segmentos previamente dibujados (aparte de los puntos extremos).

Bessie se da cuenta que para cada ~i~, ella dibujó exactamente tres segmentos nuevos. Calcule el número de permutaciones que Bessie podría haber elegido en el paso ~1~ que puedan satisfacer esta propiedad, modulo ~1\,000\,000\,007~.

Subtareas

Para el 30% de los casos de prueba se cumple que ~N \leq 8~.

Entrada

La primera línea contiene ~N~. Seguida por ~N~ líneas, cada una conteniendo dos enteros separados por espacios ~x_i~ y ~y_i~.

Salida

El número de permutaciones módulo ~1\,000\,000\,007~.

Ejemplos

Entrada 1

4
0 0
0 4
1 1
1 2

Salida 1

0

Ninguna permutación funciona.

Entrada 2

4
0 0
0 4
4 0
1 1

Salida 2

24

Todas las permutaciones sirven.

Entrada 3

5
0 0
0 4
4 0
1 1
1 2

Salida 3

96

Una permutación que satisface la propiedad es ~(0,0)~,~(0,4)~,~(4,0)~,~(1,2)~,~(1,1)~.Para esta permutación:

• Primero, ella dibuja segmentos entre cada par de ~(0,0)~,~(0,4)~, y ~(4,0)~.
• Luego ella dibuja segmentos de ~(0,0)~,~(0,4)~, y ~(4,0)~ hacia ~(1,2)~.
• Finalmente, ella dibuja segmentos de ~(1,2)~,~(4,0)~, y ~(0,0)~ a ~(1,1)~.

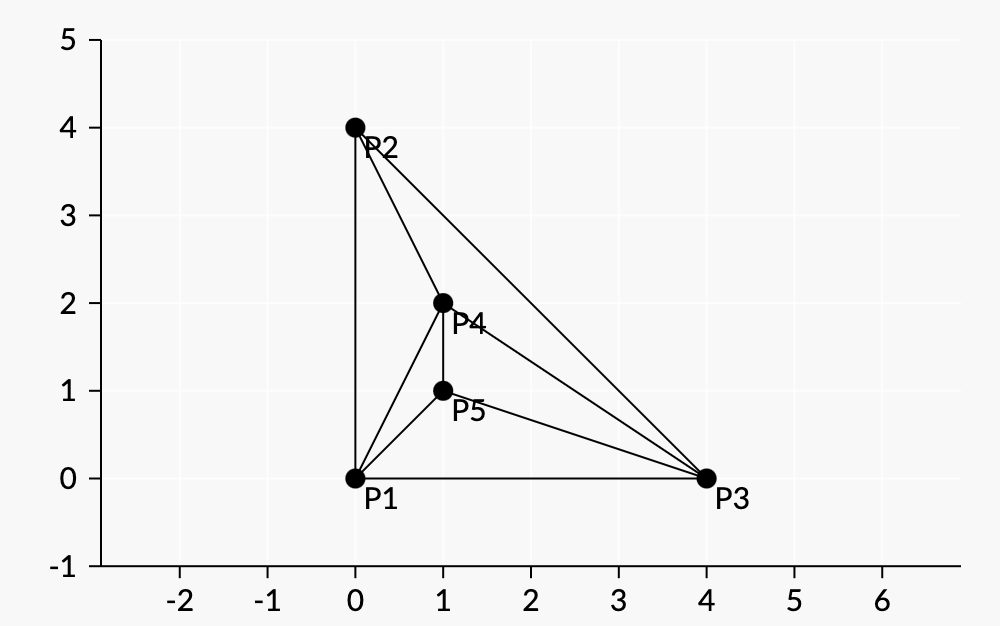
La permutación no satisface la propiedad si sus primeros cuatro puntos son ~(0,0)~, ~(1,1)~, ~(1,2)~, y ~(0,4)~ en algún orden.