Descripción

En la Ciudad Tranquila, varios ~k~ jóvenes amigos quieren participar en una manifestación de protesta. Como el barrio en el que viven es grande, se desplazarán al punto de encuentro en sus propios coches. Cada joven llevará consigo una pancarta en la que ha dibujado una sola letra de la ~A~ ... ~Z~. No habrá dos carteles con la misma letra. Las ~k~ letras forman una palabra, escribamos ~cuv~, conocido.

El barrio donde viven los jóvenes puede codificarse mediante una matriz con ~n x m~ zonas cuadradas, algunas de las cuales están prohibidas. Se sabe que un coche consume una unidad de combustible cuando se desplaza de una zona a la zona vecina y no consume combustible cuando está parado. Dos zonas son vecinas si comparten un lado.

Para ahorrar combustible, los jóvenes deciden que si dos coches se encuentran en una zona y todas las letras de los dos coches son una secuencia de la palabra, entonces continuarán el viaje en un solo coche, llevándose, por supuesto, todas las señales. En caso contrario, los coches continuarán el viaje por separado.

Por ejemplo, si la palabra cuv es "JOS", entonces el coche que lleva la letra ~J~ puede llevar al joven que lleva el signo con la letra ~O~, o viceversa: el coche que lleva la letra ~O~ puede llevar al joven que lleva la letra ~J~. Entonces el viaje puede continuar hasta el coche que lleva la letra ~S~. Alternativamente, las letras ~S~ y ~O~ pueden unirse primero en un coche, si los coches que las llevan se encuentran en la misma zona. Sin embargo, no puede producirse una transferencia, es decir, una unión de las letras, entre el coche que sólo lleva la letra ~J~ y el coche que sólo lleva la letra ~S~.

Tarea

Conocidas las dimensiones del barrio ~n~ y ~m~, la palabra ~cuv~, la configuración del barrio y las posiciones iniciales de los jóvenes, se requiere:

1. El área mínima de una submatriz de la matriz que codifica la vecindad, en la que se encuentran todas las posiciones iniciales de los jóvenes.
2. El número mínimo de unidades de combustible consumidas por todos los coches, sabiendo que al final todos los jóvenes se reunirán en un coche.

Entrada

El fichero de entrada contiene:

En la primera línea, un número natural ~p~, que sólo puede tener el valor ~1~ ó ~2~.

En la segunda línea, dos números naturales ~n~ y ~m~, separados por un espacio.

En la tercera línea, la palabra ~cuv~.

En las ~n~ líneas siguientes, ~m~ caracteres por línea que representan las zonas del distrito. Una zona está prohibida si tiene el carácter #, está libre si tiene el carácter _ (subrayado) y es el punto de partida de un coche si tiene una de las letras de la palabra ~cuv~.

Salida

Si el valor de ~p~ es ~1~, sólo se resolverá el requisito ~1~.

En este caso, en la salida se escribirá un único número natural ~A~, que representa el área mínima de una submatriz de la matriz que codifica la vecindad, en la que se encuentran todas las posiciones iniciales de los jóvenes.

Si el valor de ~p~ es ~2~, sólo se resolverá el requisito ~2~.

En este caso, en la salida se escribirá un único número natural ~C~, que representa el número mínimo de unidades de combustible consumidas por todos los coches hasta que los jóvenes, y por tanto las letras, se unan en un único coche. Si no hay solución, es decir, no se pueden juntar todos los jóvenes en un solo coche, se escribirá ~-1~.

Restricciones y aclaraciones

• 2 ≤ n, m ≤ 60
• 2 ≤ k ≤ 10
• Sea z el número de zonas prohibidas. Entonces 0 ≤ z ≤ (n * m)/3
• En cada unidad de tiempo, un coche puede permanecer parado mientras espera a otro coche, o puede desplazarse a una zona vecina, independientemente de que esa zona esté ocupada por otro coche o no.
• La longitud del lado de una zona se toma como 1.
• Por resolver correctamente el primer requisito se otorgan 20 puntos y por el segundo requisito se otorgan 80 puntos.
• En el 30% de las pruebas del requisito 2 se garantiza k ≤ 3.

Ejemplo de Entrada #1

1
4 5
JOS
#_O_#
_#__S
_#J_#
___#_

Ejemplo de Salida #1

9

Explicación de la entrada #1

La submatriz de área mínima que incluye todas las letras tiene la esquina superior izquierda en la línea ~1~ y la columna ~3~ y la esquina inferior derecha en la línea ~3~ y la columna ~5~. El área es igual al número de áreas cubiertas: ~3~ ~x~ ~3~ = ~9~.

¡Atención! Para esta prueba sólo se resuelve el requisito ~1!.

Ejemplo de Entrada #2

2
5 7
BUN
_#_#_#_
__N#__#
_#__B__
U__#_#_
_#_#_#_

Ejemplo de Salida #2

6

Explicación de la entrada #2

Una variante de consumo mínimo es: ~U~ se mueve dos posiciones a la derecha. A continuación, ~B~ se desplaza dos posiciones a la izquierda. ~U~ vuelve a subir una posición. Por último, ~N~ baja una posición. Observa que ~B~ se ha unido con ~U~, y luego BU con ~N~.

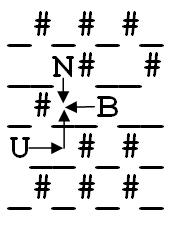
Atención. Sólo el requisito 2 está resuelto para esta prueba.

Ejemplo de Entrada #3

2
6 7
ROST
O#_#_#_
___#__#
_#_R___
____#__
__#_S_#
_#_T_#_

Ejemplo de Salida #3

9

Explicación de la entrada #3

Una variante de consumo mínimo es: ~O~ se desplaza una posición hacia abajo, luego dos posiciones hacia la derecha, baja una posición y, por último, se desplaza una posición hacia la derecha, donde se encuentra con ~R~. A continuación, ~S~ se desplaza una posición hacia la izquierda. ~T~ sube una posición y se une a ~S~. Por último, el vagón en el que se encuentran ~S~ y ~T~ sube dos posiciones y se encuentra con el vagón en el que se encuentran ~R~ y ~O~. En esta zona, en la línea ~3~ y en la columna ~4~, todas las letras se unen en un solo vagón.

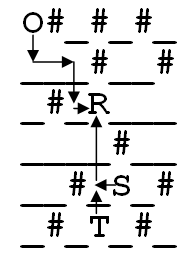
Atención. Para esta prueba sólo se resuelve el requisito 2.