Cajas
En un almacén, Rafael y Ana se encargan de introducir objetos en cajas. Para ello proceden de la forma siguiente:
- Existe un conjunto de cajas alineadas en una fila, todas ellas con la misma capacidad máxima de almacenamiento
;
- Rafael siempre está en el lado izquierdo de la fila, y Ana en el lado derecho;
- Cada uno de los dos amigos empieza a introducir los objetos en las cajas en su extremo de la fila, colocando siempre su objeto en la caja más próxima que tenga espacio suficiente (podría pasar que Rafael tuviera que usar la caja de más a la derecha, que es la primera caja de Ana, y viceversa);
- Cada uno de los dos amigos tiene una lista con un número arbitrario de objetos que debe colocar, cada uno con un determinado tamaño. Estas listas pueden tener cantidades diferentes de objetos (posiblemente cero) y cada persona debe ir colocando los objetos siguiendo el orden en el que aparecen en la lista respectiva;
- Los objetos se introducen en las cajas de forma alterna, empezando siempre por Rafael (siempre que tenga algún objeto que colocar). Así, el orden es: primer objeto de Rafael, primer objeto de Ana, segundo objeto de Rafael, etc.
Considerad el ejemplo siguiente: La capacidad de las cajas es 5; Rafael tiene dos objetos, el primero de tamaño 4 y el segundo de tamaño 2; Ana tiene dos objetos, ambos de tamaño 2. La figura siguiente ilustra lo que sucedería si existieran dos cajas para colocar los objetos:
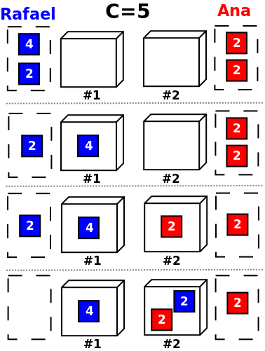
Empezamos por Rafael. El objeto de tamaño 4 se coloca en la caja de más a la izquierda, que consideraremos que es la número 1. A continuación Ana coloca su primer objeto en la caja más cercana con espacio suficiente, que es la número 2. Después es el turno de Rafael, que ahora tiene que colocar el objeto de tamaño 2. Como este no cabe en la caja 1 (solo podría caber un objeto de tamaño 1), se coloca en la caja siguiente, la 2, que tiene espacio suficiente. Por último, Ana intenta colocar su segundo objeto, pero no tiene espacio suficiente en ninguna caja. Por tanto dos cajas no son suficientes para guardar todos los objetos.
Si en cambio hubiera tres cajas, ¿acabaría con éxito este procedimiento? La figura siguiente ilustra la posición inicial y final de todos los objetos, demostrando que sí, que en este caso 3 cajas serían suficientes para guardar todos los objetos siguiendo el proceso descrito:
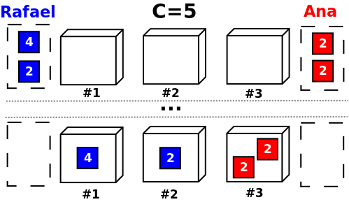
Y en un caso más general, ¿cual sería el número mínimo de cajas necesarias? Ayudad a Rafael y a Ana a ahorrar en la compra de cajas, calculando ese número.
El Problema
Dada la capacidad de cada caja, el número de objetos
de Rafael y sus tamaños
, así como el número de objetos
de Ana y sus tamaños
, hay que calcular la cantidad mínima de cajas necesarias para almacenar todos los objetos siguiendo el proceso descrito anteriormente.
Entrada
La primera línea de la entrada contiene un único entero positivo , la capacidad máxima de cada caja.
A continuación viene una línea que contiene el número
de objetos de Rafael, seguida de
líneas, cada una con un entero
, el tamaño de su objeto i-ésimo. Esta lista viene dada según el orden en el que los objetos deben ser colocados.
Después viene una línea que contiene el número
de objetos de Ana, seguido de
líneas, cada una con un entero
, el tamaño de su objeto i-ésimo. Como en el caso de Rafael, esta línea viene dada según el orden en el que los objetos deben ser colocados.
Salida
La salida debe contener una línea con el mínimo número de cajas necesarias para que el proceso descrito anteriormente termine con todos los objetos dentro de alguna caja.
Restricciones
Se garantizan los siguientes límites en todos los casos de prueba:
- \(1 \leq C \leq 1 000 000 000\) Capacidad de cada caja.
- \(0 \leq R, A \leq 50 000\) Número de objetos de Rafael y de Ana.
Tamaño de cada objeto.
Nota sobre la Evaluación: Para un conjunto de casos que valen el 30% de los puntos, siempre se cumple que y
son menores o iguales que 500. Para un conjunto de casos que valen el 60% de los puntos, siempre se cumple que
y
son menores o iguales que 5000.
Ejemplo de Entrada 1
5
2
4
2
2
2
2Ejemplo de Salida 1
3
Ejemplo de Entrada 2
5
4
3
2
1
5
3
3
4
1Ejemplo de Salida 2
5
Comments