Luego de una ardua tarea de Alfredo, ahora Valido y los informáticos se encuentran en el techo de la escuela. En este se lograron colocar un total de ~n~ ~(1\le n\le 10^5)~ antenas con el objetivo de asegurar la conexión durante la realización del concurso provincial, y ahora solo deben crear un sistema de cables que conecte la antena principal con el receptor del centro de entrenamiento.

Valido se percata que hay antenas que no se pueden conectar directamente entre ellas, y más aún, que las que permiten la conexión directa deben hacerse con un cable de un material específico. Los informáticos logran decifrar las ~m~ ~(1\le m\le 2\cdot 10^5)~ conexiones que se pueden establecer entre los pares de antenas ~u~ y ~v~ ~(1\le u,v\le 10^5)~ que lo permiten, además del material ~x~ ~(1\le x\le 10^6)~ que necesitan. Ahora deben conseguir todos los materiales necesarios para montar el sistema de cableado.

Debido a la experiencia de los informáticos, montar un sistema de cableado en último momento se ha vuelto algo trivial, por lo que ellos no necesitan saber la cantidad mínima de cables que hay que usar para este problema, sino la cantidad mínima de materiales diferentes en el sistema de cableado.

Valido estaba muy preocupado de que esta fuera una tarea muy difícil, por lo que les aseguró que cualquier conjunto de cables del mismo material se encontraba en un mismo subgrafo del grafo original, y que este subgrafo contendría solo cables de este material.

Entrada

La primera línea contiene un entero ~n~ ~(1\le n\le 10^5)~ y un entero ~m~ ~(1\le m\le 2\cdot 10^5)~, la cantidad de antenas y la cantidad de conexiones entre ellas, respectivamente.

Las siguientes ~m~ líneas contienen tres enteros ~u~,~v~ ~(1\le u,v\le n, u\neq v)~, y ~x~ ~(1\le x\le 10^6)~, significando que se pueden conectar las antenas ~u~ y ~v~ mediante un cable de material ~x~.

Le sigue una última línea con dos enteros ~a~ y ~b~ ~(1\le a,b\le n)~.

Salida

Un único entero, la menor cantidad de diferentes tipos de materiales que se necesita para conectar ~a~ con ~b~.

Ejemplo de Entrada #1

5 4
5 4 1
3 5 1
1 5 1
2 1 1
1 3

Ejemplo de Salida #1

1

Ejemplo de Entrada #2

6 10
1 2 12
4 3 40
5 6 12
1 4 40
5 3 5
1 5 5
2 6 12
4 2 40
6 4 20
3 1 40
4 5

Ejemplo de Salida #2

2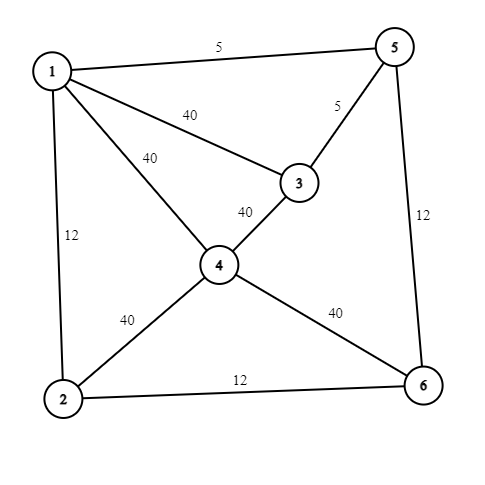

Un camino que usa la mínima cantidad de materiales diferentes puede ser ~4\rightarrow 3\rightarrow\ 5~, usando solo ~2~ materiales diferentes, el ~40~ y el ~5~.