Dado un grafo conectado no dirigido con ~N~ vértices y ~M~ aristas que no contienen auto-bucles ni aristas dobles. La i-ésima arista \((1\lei\leM)\) conecta el vértice ~a_{i}~ y el vértice ~b_{i}~.

Una arista cuya eliminación desconecta el grafo se llama puente. Encuentre el número de aristas que son puentes entre las ~M~ aristas.

Notas:

Un auto-bucle es una arista ~i~ tal que \(a_{i} = b_{i} (1\lei\leM)\). Las aristas dobles son un par de aristas ~i~, ~j~ tal que ~a_{i} = a_{j}~ y \(b_{i} = b_{j} (1\lei<j\leM)\). Se dice que un grafo no dirigido está conectado cuando existe una ruta entre cada par de vértices.

Restricciones:

\(2\leN\le50\)

\(N-1\leM\lemin(N (N - 1) / 2,50)\)

\(1\leai<bi\leN\)

El grafo dado no contiene auto-bucles ni aristas dobles.

El grafo dado está conectado.

Entrada:

Se le daran ~N~ y ~M~. Luego siguen ~N~ pares de números, la linea i-ésima contiene ~a_{i}~ y ~b_{i}~.

Salida:

Imprima el número de aristas que son puentes entre las ~M~ aristas.

Entrada de ejemplo 1:

7 7
1 3
2 7
3 4
4 5
4 6
5 6 
6 7

Salida de ejemplo 1:

4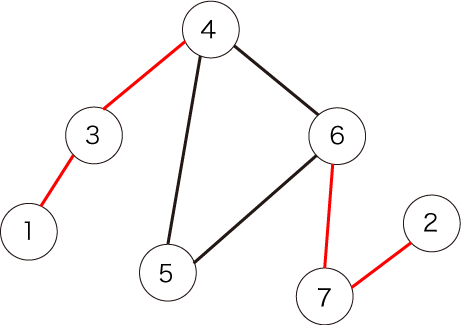

Las aristas que se muestran en rojo son puentes. Hay cuatro de ellos.

Entrada de ejemplo 2:

3 3
1 2
1 3
2 3

Salida de ejemplo 2:

0

En este ejemplo no hay puentes.

Entrada de ejemplo 3:

6 5
1 2
2 3
3 4
4 5
5 6

Salida de ejemplo 3:

5